The Triangle Distribution

These functions provide information about the triangle distribution on the interval from a to b with a maximum at c. dtriangle gives the density, ptriangle gives the distribution function, qtriangle gives the quantile function, and rtriangle generates n random deviates.

Usage

dtriangle(x, a = 0, b = 1, c = (a + b)/2)

ptriangle(q, a = 0, b = 1, c = (a + b)/2)

qtriangle(p, a = 0, b = 1, c = (a + b)/2)

rtriangle(n = 1, a = 0, b = 1, c = (a + b)/2)

Arguments

x, q

vector of quantiles.

a

lower limit of the distribution.

b

upper limit of the distribution.

c

mode of the distribution.

p

vector of probabilities.

n

number of observations. If length(n) > 1, the length is taken to be the number required.

Value

dtriangle gives the density, ptriangle gives the distribution function, qtriangle gives the quantile function, and rtriangle generates random deviates. Invalid arguments will result in return value NaN or NA.

Details

All probabilities are lower tailed probabilities. a, b, and c may be appropriate length vectors except in the case of rtriangle. rtriangle is derived from a draw from runif. The triangle distribution has density: $$f(x) = \frac{2(x-a)}{(b-a)(c-a)}$$ for \(a \le x < c\). $$f(x) = \frac{2(b-x)}{(b-a)(b-c)}$$ for \(c \le x \le b\). \(f(x) = 0\) elsewhere. The mean and variance are: $$E(x) = \frac{(a + b + c)}{3}$$ $$V(x) = \frac{1}{18}(a^2 + b^2 + c^2 - ab - ac - bc)$$

References

Becker, R. A., Chambers, J. M. and Wilks, A. R. (1988) The New S Language. Wadsworth & Brooks/Cole.

See also

.Random.seed about random number generation, runif, etc for other distributions.

Examples

## view the distribution
tri <- rtriangle(100000, 1, 5, 3)
hist(tri, breaks=100, main="Triangle Distribution", xlab="x")

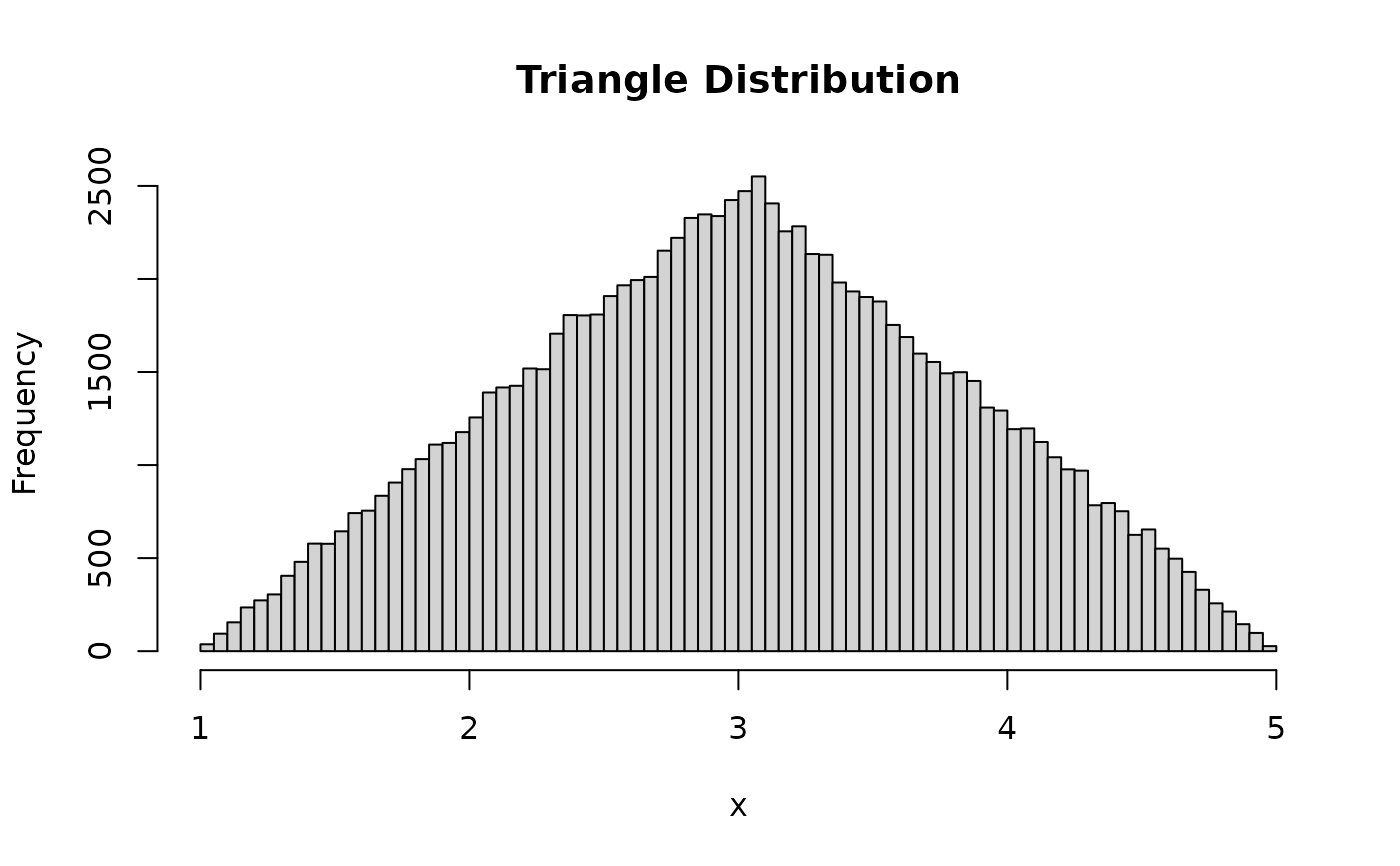mean(tri) # 1/3*(1 + 5 + 3) = 3
#> [1] 3.002157
var(tri)  # 1/18*(1^2 + 3^2 + 5^2 - 1*5 - 1*3 - 5*3) = 0.666667
#> [1] 0.6680518
dtriangle(0.5, 0, 1, 0.5) # 2/(b-a) = 2
#> [1] 2
qtriangle(ptriangle(0.7)) # 0.7
#> [1] 0.7