Latin Hypercube Samples - Questions

Rob Carnell

2024-06-30

Source: vignettes/lhs_faq.Rmd

Question 1

I am looking for a package which gives me Latin hypercube samples from a grid of values:

a <- (1:10) 
b <- (20:30) 
dataGrid <- expand.grid(a, b)

Answer

The lhs package returns a uniformly distributed stratified sample from the unit hypercube. The marginal distributions can then be transformed to your distribution of choice. If you wanted a uniform Latin hypercube on [1,10] and [20,30] with 22 samples, you could do:

X <- randomLHS(22, 2) 
X[,1] <- 1 + 9*X[,1] 
X[,2] <- 20 + 10*X[,2] 

# OR 

Y <- randomLHS(22, 2) 
Y[,1] <- qunif(Y[,1], 1, 10) 
Y[,2] <- qunif(Y[,2], 20, 30) 

head(X)
#>          [,1]     [,2]
#> [1,] 9.360227 21.96763
#> [2,] 4.808267 28.84202
#> [3,] 1.960651 27.97779
#> [4,] 7.200957 21.79375
#> [5,] 1.200379 28.40089
#> [6,] 4.091125 24.84824
head(Y)
#>          [,1]     [,2]
#> [1,] 8.284968 29.24988
#> [2,] 5.525437 28.53956
#> [3,] 8.981331 27.07328
#> [4,] 2.887880 23.40239
#> [5,] 1.730310 29.07440
#> [6,] 7.708760 27.45095

If you want integers only in the sample, then you can use qinteger.

X <- randomLHS(3, 2)
X[,1] <- qinteger(X[,1], 1, 10)
X[,2] <- qinteger(X[,2], 20, 30)

head(X)
#>      [,1] [,2]
#> [1,]    4   24
#> [2,]    8   28
#> [3,]    5   20

Question 2

I am trying to do a Latin hypercube Sampling (LHS) to a 5-parameter design matrix. I want the combination of the first three parameters to sum up to 1 (which obviously do not)

If I divide each of these parameters with the sum, the uniform distribution is lost. Is there a way to maintain the random LHS (with uniformly distributed parameters) so that the referred condition is fulfilled?

Answer

In my experience with Latin hypercube samples, most people draw the sample on a uniform hypercube and then transform the uniform cube to have new distributions on the margins. The transformed distributions are not necessarily uniform. It is possible to draw a Latin hypercube with correlated margins and have them sum to one using qdirichlet, but they will not be uniform. I’ll make a quick example argument that explains the difficulty…

In two dimensions, you could draw this which is uniform and correlated.

x <- seq(0.05, 0.95, length = 10) 
y <- 1 - x 
all.equal(x + y, rep(1, length(x))) 
#> [1] TRUE
hist(x, main = "") 

hist(y, main = "")

But in three dimensions, it is hard to maintain uniformity because large samples on the first uniform margin overweight the small samples on the other margins.

x <- seq(0.05, 0.95, length = 10) 
y <- runif(length(x), 0, 1 - x) 
z <- 1 - x - y 
hist(x, main = "") 

hist(y, main = "")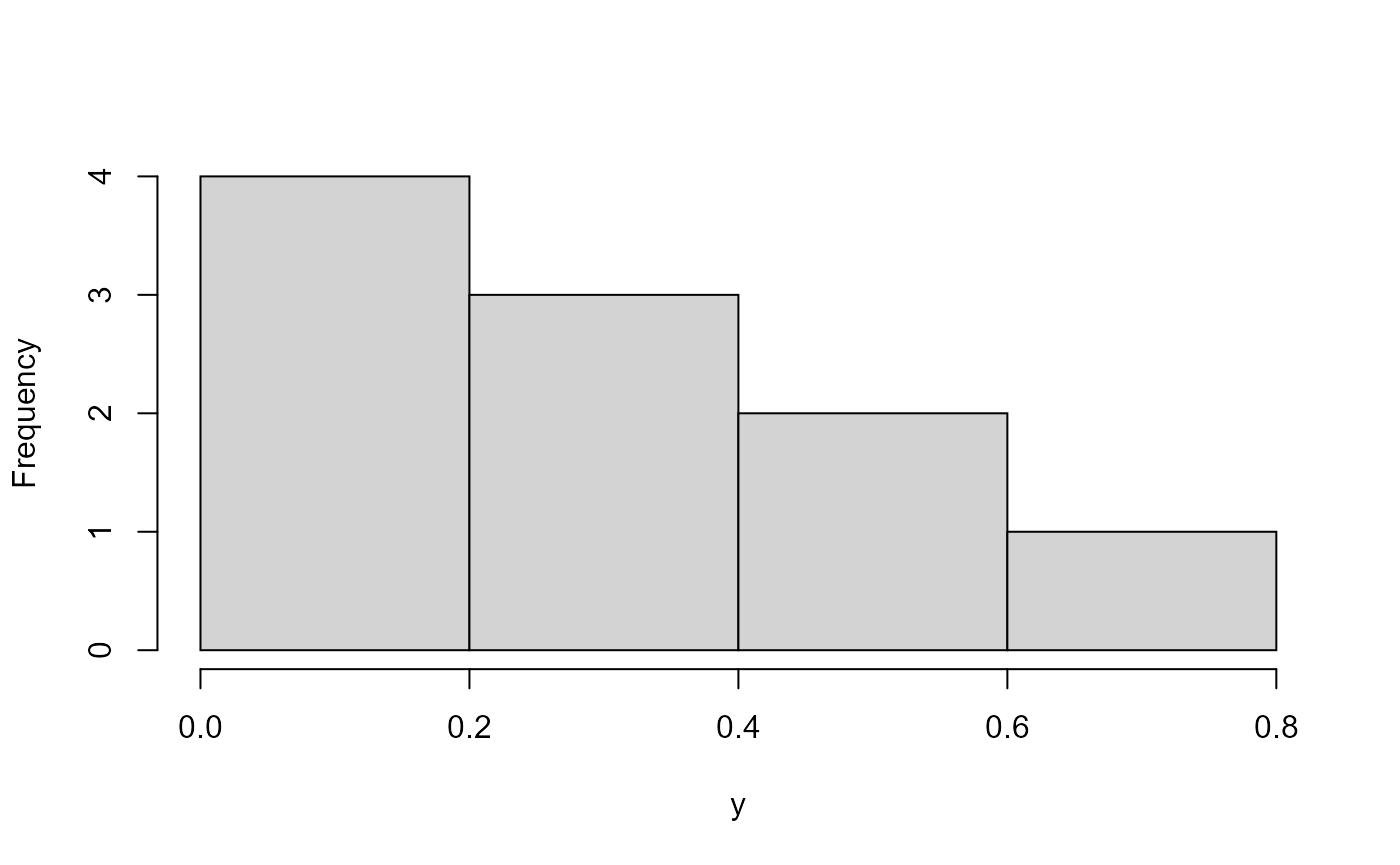 

hist(z, main = "")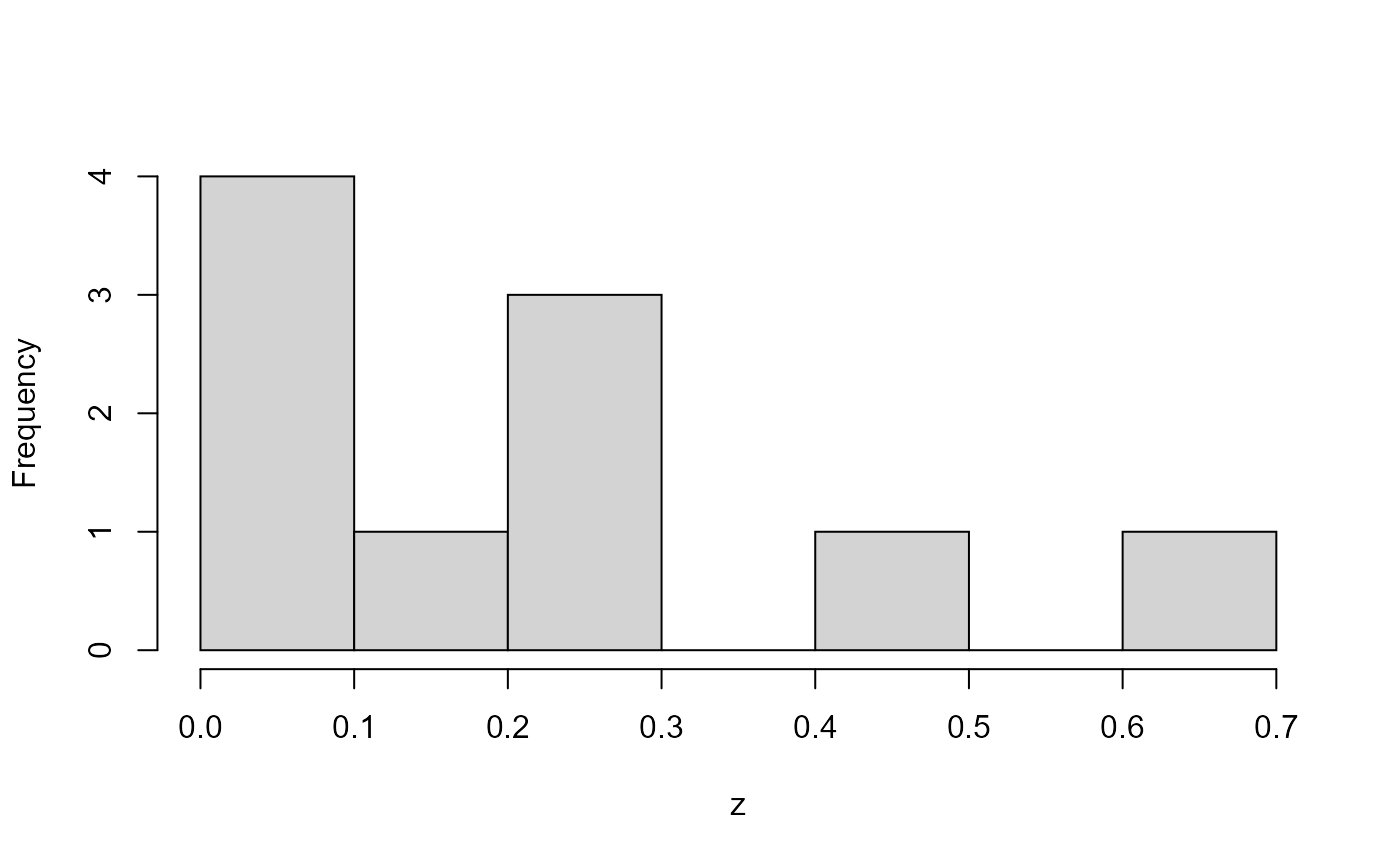

The transformed distributions maintain their “Latin” properties, but are in the form of new distributions. The Dirichlet distribution is built for this purpose.

N <- 1000
x <- randomLHS(N, 5) 
y <- x 
y[,1:3] <- qdirichlet(x[,1:3], c(1, 1, 1))
y[,4] <- x[,4] 
y[,5] <- x[,5] 

par(mfrow = c(2,3)) 
dummy <- apply(x, 2, hist, main = "") 

par(mfrow = c(2,3)) 

dummy <- apply(y, 2, hist, main = "") 

all.equal(rowSums(y[,1:3]), rep(1, nrow(y))) 
#> [1] TRUE

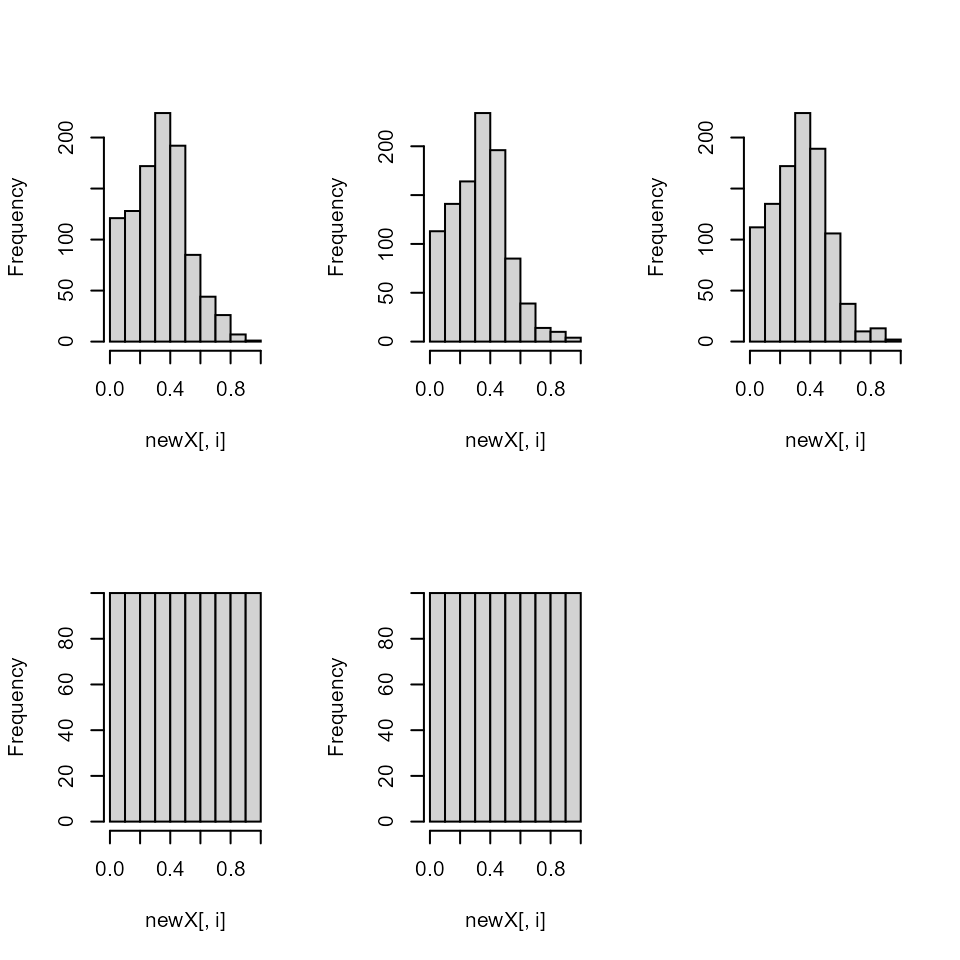
The uniform properties are gone as you can see here…

par(mfrow = c(1,1)) 
pairs(x) 

pairs(y, col = "red")

Question 3

How do I create a Latin hypercube that ranges between between 0 and 1 and sums to 1?

Answer

I have a solution to this problem using a Dirichlet distribution.
The result is not uniformly distributed on (0,1) anymore, but instead is Dirichlet distributed with the parameters alpha. The Latin properties are maintained.

X <- randomLHS(1000, 7) 
Y <- qdirichlet(X, rep(1,7)) 
stopifnot(all(abs(rowSums(Y) - 1) < 1E-12)) 
range(Y) 
#> [1] 5.076098e-06 8.393811e-01

ws <- randomLHS(1000, 7) 
wsSums <- rowSums(ws) 
wss <- ws / wsSums 
stopifnot(all(abs(rowSums(wss) - 1) < 1E-12)) 
range(wss)
#> [1] 2.648948e-05 5.038924e-01

Question 5

I need to use Latin hypercube sampling for my own custom functions.

Answer 

require(lhs) 

# functions you described 
T1 <- function(t) t*t 
WL1 <- function(T1, t) T1*t 
BE1 <- function(WL1, T1, t) WL1*T1*t 

# t is distributed according to some pdf (e.g. normal) 
# draw a lhs with 512 rows and 3 columns (one for each function) 
y <- randomLHS(512, 3) 
# transform the three columns to a normal distribution (these could be any 
# distribution) 
t <- apply(y, 2, function(columny) qnorm(columny, 2, 1)) 
# transform t using the functions provided 
result <- cbind( 
  T1(t[,1]), 
  WL1(T1(t[,2]), t[,2]), 
  BE1(WL1(T1(t[,3]), t[,3]), T1(t[,3]), t[,3]) 
) 
# check the results 
# these should be approximately uniform 
par(mfrow = c(2,2)) 
dummy <- apply(y, 2, hist, breaks = 50, main = "") 
# these should be approximately normal 
par(mfrow = c(2,2)) 

dummy <- apply(t, 2, hist, breaks = 50, main = "") 
# these should be the results of the functions 
par(mfrow = c(2,2)) 

dummy <- apply(result, 2, hist, breaks = 50, main = "")

Question 6

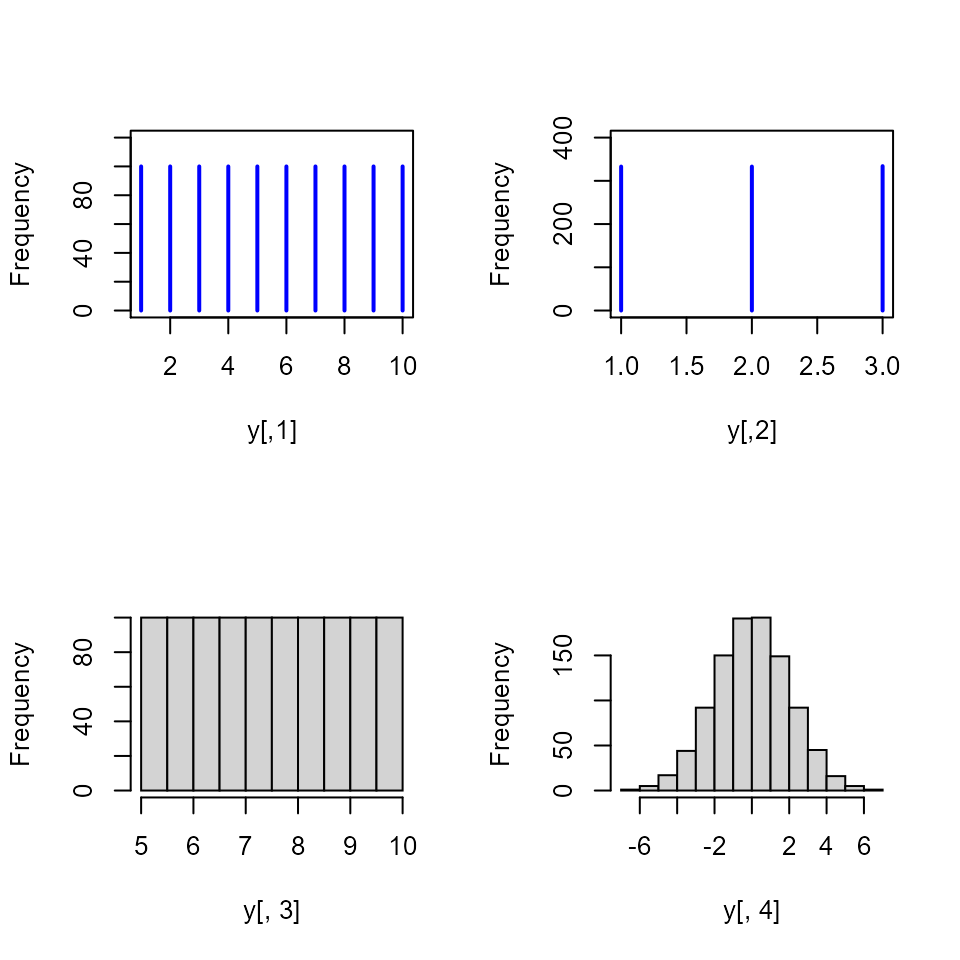
I need a Latin hypercube sample on an integer set or a set of colors.

Answer 

N <- 1000 

x <- randomLHS(N, 4) 
y <- as.data.frame(x) 
# uniform integers on 1-10 
y[,1] <- qinteger(x[,1], 1, 10)
# three colors 1,2,3 
y[,2] <- qfactor(x[,2], factor(c("R", "G", "B"))) 
# other distributions 
y[,3] <- qunif(x[,3], 5, 10) 
y[,4] <- qnorm(x[,4], 0, 2) 

table(y[,1])
#> 
#>   1   2   3   4   5   6   7   8   9  10 
#> 100 100 100 100 100 100 100 100 100 100
table(y[,2])
#> 
#>   B   G   R 
#> 334 333 333

hist(y[,3], main="") 

hist(y[,4], main="")